Unsupervised Learning | Clustering

In the last blog we discussed supervised machine learning and K-Nearest neighbour technique to solve the classification problem. If you haven’t read the previous blog, it is recommended you read it first.

In this blog we will discuss another important aspect of machine learning, called as Unsupervised learning. As the name suggests there is no supervision provided from the programmer. Unlike Supervised learning, the algorithms, generally, take the raw input and transform it into something meaningful. Let’s start with a general example from daily life. Suppose you are given a basket of fruits (containing apples, strawberries, Guavas and grapes) and asked to categorise different type of fruits with no information whatsoever. This type of problem is referred as Clustering problem.

The first step to solve any machine learning problem is to extract the features from the data. We will take only two features for the fruits, namely colour and volume. For sake of simplicity, the colour feature will be a discrete set of natural colours (unlike taking RGB values at each pixel). Then we put the fruits on a 2-dimensional graph, where x-axis indicates the colour and y-axis indicate the size. The 2-dimensional representation of our fruit data is shown in Image1.

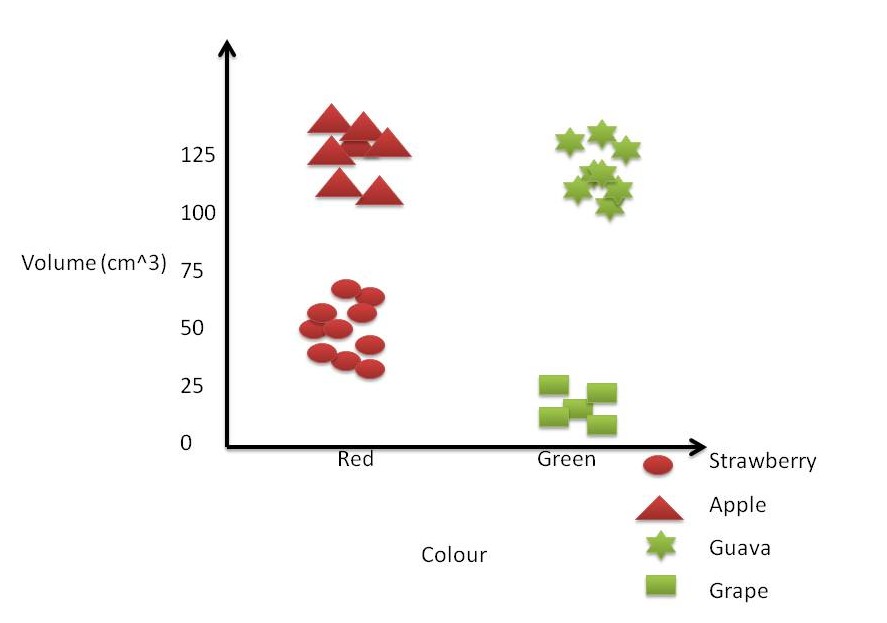
Figure 1. Sample 2-dimensional representation of fruits

For a moment forget the categories of fruit and just look at the image representing the fruits on a 2-dimensional plane. It is evident by looking at the image that there are 4 inherent clusters in the image. Remember that in most of real case examples, the distinction is not very clear.

There are a number of clustering techniques in use today, but perhaps the most famous technique used is called K-means clustering. It is an iterative algorithm which learns about the data with each successive iteration. It computes two quantities in each iteration, namely “within-cluster” distance and “between-cluster” distance. The distance between objects belonging to same cluster should be as low as possible and similarly the distance between centroids of every cluster should be as large as possible. Every successive iteration measures the value change for these two metrics and the algorithm stops when change in these quantities become zero or very small. This algorithm will result in clear-cut distinction between the clusters which allows us to group similar things together in one cluster.

In our next blog, we will cover K-means clustering in detail with pseudo-code and examples.